
§2. The Triad in Reasoning 1)
369. Kant, the King of modern thought, it was who first remarked the frequency in logical analytics of trichotomics or threefold distinctions. It really is so; I have tried hard and long to persuade myself that it is only fanciful, but the facts will not countenance that way of disposing of the phenomenon. Take any ordinary syllogism:
All men are mortal,
Elijah was a man;
Therefore, Elijah was mortal.
There are here three propositions, namely, two premisses and a conclusion; there are also three terms, man, mortal, and Elijah. If we transpose one of the premisses with the conclusion, denying both, we obtain what are called the indirect figures of syllogism; for example
All men are mortal,
But Elijah was not mortal;
Therefore, Elijah was not a man.
Elijah was not mortal,
But Elijah was a man;
Therefore, some men are not mortal.
Thus, there are three figures of ordinary syllogism. It is true there are other modes of inference which do not come under any of these heads; but that does not annul the fact that we have here a trichotomy. Indeed, if we examine by itself what is by some logicians called the fourth figure, we find that it also has three varieties related to one another as the three figures of ordinary syllogism. There is an entirely different way of conceiving the relations of the figures of syllogism; namely, by means of the conversion of propositions. But from that point of view also, the same classes are preserved. DeMorgan1) has added a large number of new syllogistic moods which do not find places in this classification. The reasoning in these is of a peculiar character and introduces the principle of dilemma. Still, regarding these dilemmatic reasonings by themselves, they fall into three classes in a precisely similar manner.
Again, I have shown2) that the probable and approximate inferences of science must be classified on the very same principles, being either Deductions, Inductions, or Hypotheses. Other examples of threes in logic are statements of what is actual, what is possible, and what is necessary; the three kinds of forms, Names,3) Propositions, and Inferences;4) affirmative, negative, and uncertain answers to a question. One very important triad is this: it has been found that there are three kinds of signs which are all indispensable in all reasoning; the first is the diagrammatic sign or icon, which exhibits a similarity or analogy to the subject of discourse; the second is the index, which like a pronoun demonstrative or relative, forces the attention to the particular object intended without describing it; the third [or symbol] is the general name or description which signifies its object by means of an association of ideas or habitual connection between the name and the character signified.
370. But there is one triad in particular which throws a strong light on the nature of all the others. Namely, we find it necessary to recognize in logic three kinds of characters, three kinds of facts. First there are singular characters which are predicable of single objects, as when we say that anything is white, large, etc. Secondly, there are dual characters which appertain to pairs of objects; these are implied by all relative terms as »lover,« »similar,« »other,« etc. Thirdly, there are plural characters, which can all be reduced to triple characters but not to dual characters. Thus, we cannot express the fact that A is a benefactor of B by any descriptions of A and B separately; we must introduce a relative term. This is requisite, not merely in English, but in every language which might be invented. This is true even of such a fact as A is taller than B. If we say, »A is tall, but B is short,« the conjugation »but« has a relative force, and if we omit this word the mere collocation of the two sentences is a relative or dual mode of signifying. . . .
371. Let us now consider a triple character, say that A gives B to C. This is not a mere congeries of dual characters. It is not enough to say that A parts with C, and that B receives C. A synthesis of these two facts must be made to bring them into a single fact; we must express that C, in being parted with by A, is received by B. If, on the other hand, we take a quadruple fact, it is easy to express as a compound of two triple facts. . . . We are here able to express the synthesis of the two facts into one, because a triple character involves the conception of synthesis. Analysis involves the same relations as synthesis; so that we may explain the fact that all plural facts can be reduced to triple facts in this way. A road with a fork in it is the analogue of a triple fact, because it brings three termini into relation with one another. A dual fact is like a road without a fork; it only connects two termini. Now, no combination of roads without forks can have more than two termini; but any number of termini can be connected by roads which nowhere have a knot of more than three ways. See the
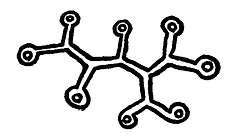
figure, where I have drawn the termini as self-returning roads, in order to introduce nothing beyond the road itself. Thus, the three essential elements of a network of roads are road about a terminus, roadway-connection, and branching; and in like manner, the three fundamental categories of fact are, fact about an object, fact about two objects (relation), fact about several objects (synthetic fact).
372. We have seen that the mere coexistence of two singular facts constitutes a degenerate form of dual fact; and in like manner there are two orders of degeneracy in plural facts, for either they may consist in a mere synthesis of facts of which the highest is dual, or they may consist in a mere synthesis of singular facts. This explains why there should be three classes of signs; for there is a triple connection of sign, thing signified, cognition produced in the mind. There may be a mere relation of reason between the sign and the thing signified; in that case the sign is an icon. Or there may be a direct physical connection; in that case, the sign is an index. Or there may be a relation which consists in the fact that the mind associates the sign with its object; in that case the sign is a name1) [or symbol]. Now consider the difference between a logical term, a proposition, and an inference. A term is a mere general description, and as neither icon nor index possesses generality, it must be a name; and it is nothing more. A proposition is also a general description, but it differs from a term in that it purports to be in a real relation to the fact, to be really determined by it; thus, a proposition can only be formed of the conjunction of a name and an index. An inference, too, contains a general description. . . .


